Distribusi
frekuensi relative
Nilai frekuensinya TIDAK dinyatakan dalam bentuk ANGKA MUTLAK, tapi dalam bentuk ANGKA PERSENTASE (%) atau ANGKA RELATIF.
Nilai frekuensinya TIDAK dinyatakan dalam bentuk ANGKA MUTLAK, tapi dalam bentuk ANGKA PERSENTASE (%) atau ANGKA RELATIF.
Rumus mencari frekuensi relatif adalah :

Contoh:
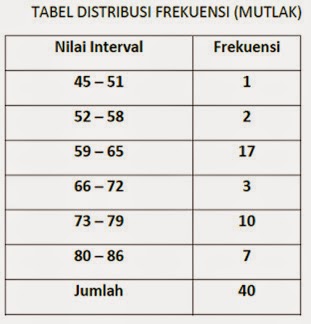
Maka, untuk membuat tabel
distribusi frekuensi relatif (%) adalah dengan mencari frekuensi relatif (%)
untuk setiap interval kelasnya dulu.
Jawab :
f relatif kelas ke-1 = 1/40 x 100% = 2,5%
f relatif kelas ke-2 = 2/40 x 100% = 5%
f relatif kelas ke-3 = 17/40 x 100% = 42,5%
f relatif kelas ke-4 = 3/40 x 100% = 7,5%
f relatif kelas ke-5 = 10/40 x 100% = 25%
f relatif kelas ke-6 = 7/40 x 100% = 17,5% +
Total
= 100%
Lalu masukkan hasil perhitungan frekuensi relatif tersebut ke dalam tabel.
Lalu masukkan hasil perhitungan frekuensi relatif tersebut ke dalam tabel.

Distribusi frekuensi kumulatif
Distribusi Frekuensi
Kumulatif (fkum ) adalah distribusi yang nilai frekuensinya (f) diperoleh
dengan cara MENJUMLAHKAN frekuensi demi frekuensi.
Distribusi Frekuensi Kumulatif terbagi menjadi 2, yaitu :
Distribusi Frekuensi Kumulatif terbagi menjadi 2, yaitu :
- Distribusi Frekuensi Kumulatif “KURANG DARI”
- Distribusi Frekuensi Kumulatif “ATAU LEBIH”
Contoh
- Distribusi Frekuensi Kumulatif “ATAU LEBIH”
Contoh
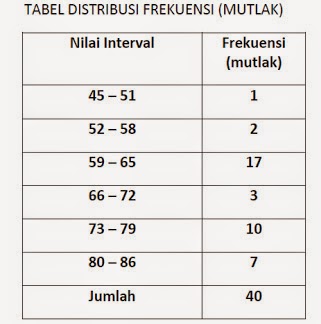
Dengan mengacu pada tabel Distribusi Frekuensi Mutlak di atas, maka contoh Tabel Distribusi Frekuensi Kumulatif nya :
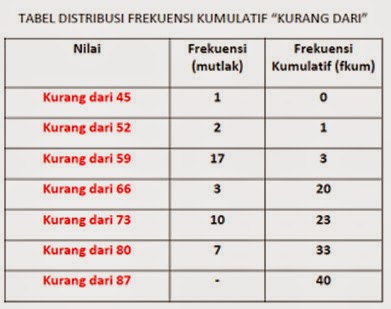
Keterangan Tabel Distribusi Frekuensi Kumulatif “KURANG DARI” :
- Untuk
acuan penentuan nilai, menggunakan nilai ujung bawah kelas.
- Penentuan
frekuensi kumulatif melihat dari frekuensi pada tabel distribusi frekuensi
(mutlak) lalu dikumulasikan sesuai dengan kategori nilai pada tabel distribusi
frekuensi kumulatif.
- Ada
penambahan 1 kelas, yaitu “KURANG DARI 87” dikarenakan nilai data terbesar
adalah 85, sehingga kalau nilai “KURANG DARI” hanya sampai ke “KURANG DARI 80”
saja, maka untuk data nilai yang LEBIH DARI 80 tidak masuk hitungan padahal ada
frekuensinya.
Sedangkan untuk Distribusi
Frekuensi Kumulatif “ATAU LEBIH”, contohnya adalah :

Keterangan Tabel Distribusi Frekuensi Kumulatif “ATAU LEBIH”
-Konsep perhitungan
frekuensi kumulatifnya sama dengan frekuensi kumulatif “KURANG DARI”, hanya
saja kalau tabel distribusi frekuensi kumulatif “ATAU LEBIH” mengacu pada nilai
“ATAU LEBIH” nya, sehingga kita tinggal mencari berapa frekuensi kumulatifnya
dengan melihat dari frekuensi (mutlak).
DISTRIBUSI FREKUENSI KUMULATIF RELATIF
DISTRIBUSI FREKUENSI KUMULATIF RELATIF
Distribusi Frekuensi
Kumulatif Relatif {fkum (%)} adalah distribusi frekuensi yang NILAI FREKUENSI
KUMULATIF diubah menjadi NILAI FREKUENSI RELATIF atau dalam bentuk persentase
(%).
Distribusi Frekuensi Kumulatif Relatif juga terbagi menjadi :
Distribusi Frekuensi Kumulatif Relatif juga terbagi menjadi :
-Distribusi Frekuensi
Kumulatif Relatif “KURANG DARI”
-Distribusi Frekuensi
Kumulatif Relatif “ATAU LEBIH”
Konsep Distribusi
Frekuensi Kumulatif Relatif adalah :
-TIDAK menggunakan angka
mutlak, jadi menggunakan persentase.
-Mengambil frekuensinya
dari tabel DISTRIBUSI FREKUENSI KUMULATIF.
Rumus untuk mencari
Frekuensi Kumulatif Relatif (%) adalah :

Contoh

Dengan mengacu pada tabel distribusi frekuensi kumulatif “KURANG DARI” di atas, maka perhitungan frekuensi kumulatif relatifnya adalah :
F kum (%) kelas ke-1 = 0/40 x 100% = 0 %
F kum (%) kelas ke-2 = 1/40 x 100% = 2,5%
F kum (%) kelas ke-3 = 3/40 x 100% = 7,5%
F kum (%) kelas ke-4 = 20/40 x 100% = 50%
F kum (%) kelas ke-5 = 23/40 x 100% = 57,5%
F kum (%) kelas ke-6 = 33/40 x 100% = 82,5%
F kum (%) kelas ke-7 = 40/40 x 100% = 100%
Dari perhitungan di atas lalu dimasukkan ke dalam tabel.

Untuk Distribusi Frekuensi Kumulatif Relatif “ATAU LEBIH” juga sama rumus perhitungannya.
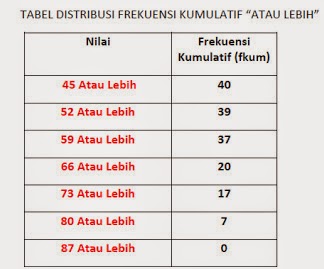
Dari tabel distribusi frekuensi kumulatif “ATAU LEBIH” di atas, bisa dilakukan perhitungan untuk mencari Frekuensi Kumulatif Relatif “ATAU LEBIH” :
F kum (%) kelas ke-1 = 40/40 x 100% = 100%
F kum (%) kelas ke-2 = 39/40 x 100% = 97,5 %
F kum (%) kelas ke-3 =
37/40 x 100% = 92,5 %
F kum (%) kelas ke-4 = 20/40 x 100% = 50%
F kum (%) kelas ke-5 = 17/40 x 100% = 42,5 %
F kum (%) kelas ke-6 = 7/40 x 100% =7,5 %
F kum (%) kelas ke-7 = 0/40 x 100% = 0%
Setelah selesai melakukan perhitungan, lalu masukkan hasilnya ke dalam tabel
distribusi frekuensi kumulatif relatif “ATAU LEBIH”.

Grafik merupakan lukisan pasang surutnya suatu keadaan dengan garis atau gambar atau dengan kata lain, Grafik menggambarkan naik atau turunnya hasil statistik.
Dengan masih mengacu pada
Tabel Distribusi Frekuensi, maka bisa digambarkan dengan cara membuat grafik :
* Histogram
* Poligon Frekuensi
* Ogive
HISTOGRAM
-Histogram merupakan
grafik yang menggambarkan suatu distribusi frekuensi dengan bentuk beberapa
segiempat atau menyerupai diagram batang.
-Langkah-langkah membuat
Histogram :
-Buat “absis” dan
“ordinat” . absis adalah sumbu mendatar atau sumbu X yang menyatakan
NILAI; ordinat adalah sumbu tegak atau sumbu Y yang menyatakan FREKUENSI.
-Buat skala absis dan
skala ordinatnya dengan melihat dari nilai dan frekuensinya.
-Buat Batas Kelas
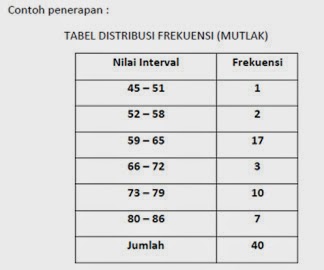
Batas Kelas :
Batas kelas ke-1 : 45 – 0,5 = 44,5
Batas kelas ke-2 : ( 51 + 52) x ½ = 51,5
Batas kelas ke-3 : (58 + 59) x ½ = 58,5
Batas kelas ke-4 : (65+66) x ½ = 65,5
Batas kelas ke-5 : (72+73) x ½ = 72,5
Batas kelas ke-6 : (79+80) x ½ = 79,5
Batas kelas ke-7 : 86 + 0,5 = 86,5
Lalu masukkan ke dalam tabel dan sesuaikan dengan frekuensinya.
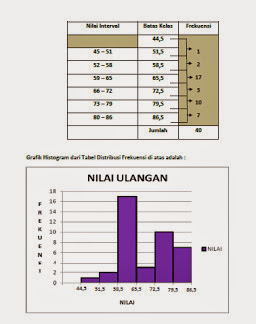
POLIGON FREKUENSI
- Poligon Frekuensi
merupakan grafik garis yang menghubungkan NILAI TENGAH tiap sisi atas yang
berdekatan dengan NILAI TENGAH jarak frekuensi mutlak masing-masing.
-Perbedaan antara HISTOGRAM dengan POLIGON FREKUENSI adalah :
*Histogram menggunakan BATAS KELAS ; sedangkan POLIGON menggunakan TITIK TENGAH.
*Grafik HISTOGRAM berwujud SEGIEMPAT atau menyerupai DIAGRAM BATANG; sedangkan POLIGON berwujud GARIS atau KURVA yang saling berhubungan satu sama lain.
-Langkah-langkah membuat POLIGON FREKUENSI :
*Buat TITIK TENGAH kelas dengan cara : (NILAI UJUNG BAWAH KELAS + NILAI UJUNG ATAS KELAS) x ½
*Buat TABEL DISTRIBUSI FREKUENSI yang MUTLAK disertai dengan kolom tambahan berupa kolom TITIK TENGAH KELAS tsb.
*Buat grafik poligon frekuensi dengan melihat data pada tabel distribusi frekuensi mutlak
-Perbedaan antara HISTOGRAM dengan POLIGON FREKUENSI adalah :
*Histogram menggunakan BATAS KELAS ; sedangkan POLIGON menggunakan TITIK TENGAH.
*Grafik HISTOGRAM berwujud SEGIEMPAT atau menyerupai DIAGRAM BATANG; sedangkan POLIGON berwujud GARIS atau KURVA yang saling berhubungan satu sama lain.
-Langkah-langkah membuat POLIGON FREKUENSI :
*Buat TITIK TENGAH kelas dengan cara : (NILAI UJUNG BAWAH KELAS + NILAI UJUNG ATAS KELAS) x ½
*Buat TABEL DISTRIBUSI FREKUENSI yang MUTLAK disertai dengan kolom tambahan berupa kolom TITIK TENGAH KELAS tsb.
*Buat grafik poligon frekuensi dengan melihat data pada tabel distribusi frekuensi mutlak
Contoh

a. Buat TITIK TENGAH KELAS
Titik tengah kelas ke-1 : (45 + 51) x ½ = 48
Titik tengah kelas ke-2 : (52 + 58) x ½ = 55
Titik tengah kelas ke-3 : (59 + 65) x ½ = 62
Titik tengah kelas ke-4 : (66 + 72) x ½ = 69
Titik tengah kelas ke-5 : (73 + 79) x ½ = 76
Titik tengah kelas ke-6 : (80 + 86) x ½ = 83
b. Buat Tabel Distribusi
Frekuensi Mutlak dengan menambah kolom TITIK TENGAH KELAS

c. Buat grafik poligon
frekuensi

OGIVE
-Ogive biasanya digunakan untuk sensus penduduk tentang perkembangan kelahiran dan kematian bayi, perkembangan penjualan suatu produk, perkembangan dan penjualan saham, dsb.
-Ogive biasanya digunakan untuk sensus penduduk tentang perkembangan kelahiran dan kematian bayi, perkembangan penjualan suatu produk, perkembangan dan penjualan saham, dsb.
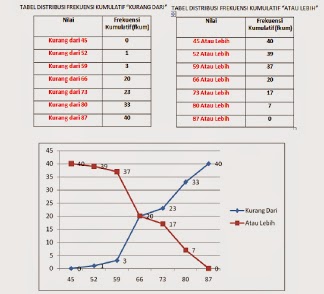
Contoh Penerapan Grafik Ogive
1. Grafik Ogive berdasarkan dari Tabel Distribusi Frekuensi Kumulatif “KURANG DARI” dan Tabel Distribusi Frekuensi Kumulatif “ATAU LEBIH”.
1. Grafik Ogive berdasarkan dari Tabel Distribusi Frekuensi Kumulatif “KURANG DARI” dan Tabel Distribusi Frekuensi Kumulatif “ATAU LEBIH”.
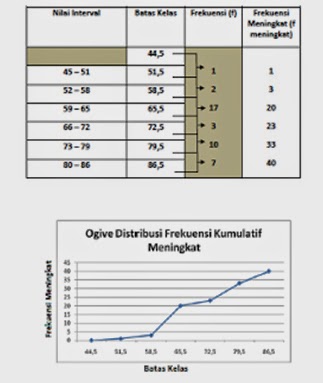
2. Grafik Ogive dari Tabel
Distribusi Frekuensi (mutlak) ditambah dengan 1 kolom FREKUENSI MENINGKAT
dengan menggunakan BATAS KELAS (Batas nyata).










No comments:
Post a Comment