Trigonometri (dari bahasa Yunani trigonon = tiga sudut dan metro = mengukur) adalah sebuah cabang matematika yang berhadapan dengan sudut segitiga dan fungsi trigonometrik seperti sinus, cosinus, dan tangen. Trigonometri memiliki hubungan dengan geometri, meskipun ada ketidaksetujuan tentang apa hubungannya; bagi beberapa orang, trigonometri adalah bagian dari geometri.
Sejarah awal
Awal trigonometri dapat dilacak hingga zaman Mesir Kuno dan Babilonia dan peradaban Lembah Indus, lebih dari 3000 tahun yang lalu. Matematikawan India adalah perintis penghitungan variabel aljabar yang digunakan untuk menghitung astronomi dan juga trigonometri. Lagadha adalah matematikawan yang dikenal sampai sekarang yang menggunakan geometri dan trigonometri untuk penghitungan astronomi dalam bukunya Vedanga, Jyotisha, yang sebagian besar hasil kerjanya hancur oleh penjajah India.
Matematikawan Yunani Hipparchus sekitar 150 SM menyusun tabel trigonometri untuk menyelesaikan segitiga.
Matematikawan Yunani lainnya, Ptolemy sekitar tahun 100 mengembangkan penghitungan trigonometri lebih lanjut.
Matematikawan Silesia Bartholemaeus Pitiskus menerbitkan sebuah karya yang berpengaruh tentang trigonometri pada 1595 dan memperkenalkan kata ini ke dalam bahasa Inggris dan Perancis.
Konsep Trigonometri
Dasar dari Trigonometri adalah Konsep kesebangunan segitiga siku-siku. Sisi-sisi yang bersesuaian pada dua bangun datar yang sebangun memiliki perbandingan yang sama. Pada geometri Euclid, jika masing-masing sudut pada dua segitiga memiliki besar yang sama, maka kedua segitiga itu pasti sebangun.[1] Hal ini adalah dasar untuk perbandingan trigonometri sudut lancip. Konsep ini lalu dikembangkan lagi untuk sudut-sudut non lancip (lebih dari 90 derajat dan kurang dari nol derajat).
Trigonometri sekarang ini
Ada banyak aplikasi trigonometri. Terutama adalah teknik triangulasi yang digunakan dalam astronomi untuk menghitung jarak ke bintang-bintang terdekat, dalam geografi untuk menghitung antara titik tertentu, dan dalam sistem navigasi satelit.
Bidang lainnya yang menggunakan trigonometri termasuk astronomi (dan termasuk navigasi, di laut, udara, dan angkasa), teori musik, akustik, optik, analisis pasar finansial, elektronik, teori probabilitas, statistika, biologi, pencitraan medis/medical imaging (CAT scan dan ultrasound), farmasi, kimia, teori angka (dan termasuk kriptologi), seismologi, meteorologi, oseanografi, berbagai cabang dalam ilmu fisika, survei darat dan geodesi, arsitektur, fonetika, ekonomi, teknik listrik, teknik mekanik, teknik sipil, grafik komputer, kartografi, kristalografi.
Ada pengembangan modern trigonometri yang melibatkan "penyebaran" dan "quadrance", bukan sudut dan panjang. Pendekatan baru ini disebut trigonometri rasional dan merupakan hasil kerja dari Dr. Norman Wildberger dari Universitas New South Wales.
A. Berikut ini adalah fungsi dasarnya (sinus, cosinus, tangen):
Pada segitiga ABC di samping, dengan panjang AB adalah q, BC = p, dan AC = r, serta sudut CAB = X, maka berlaku:
B. identitas trigonometri

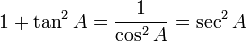

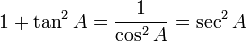


D. Perbandingan Trigonometri sudut berelasi
Perbandingan trigonometri sudut berelasi dapat dicari dengan menggunakan bantuan lingkaran satuan seperti pada gambar 3
1. Sudut berelasi (90º – a)
a) sin(90º – a) = cos a
b) cos(90º – a) = sin a
c) tan(90º – a) = cot a
2. Sudut berelasi (180º – a)
a) sin(180º – a) = sin a
b) cos(180º – a) = – cos a
c) tan(180º – a) = – tan a
3. Sudut berelasi (270º – a)
a) sin(270º – a) = – cos a
b) cos(270º – a) = – sin a
c) tan(270º – a) = cot a
4. Sudut berelasi (– a)
a) sin(– a) = – sin a
b) cos(– a) = cos a
c) tan(– a) = – tan a
| 
gambar 3
|
- E. Rumus–Rumus dalam Segitiga
- Aturan sinus :Aturan sinus digunakan apabila kondisi segitiganya adalah:


- Aturan Kosinus : a2 = b2 + c2 – 2bc cos A

- F. Rumus Penjumlahan
-
- G. Rumus Sudut Rangkap Dua

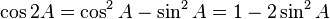 ,
,
- H. Rumus Sudut Rangkap Tiga

- I. Rumus Setengah Sudut
3. Luas segitiga


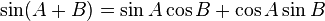
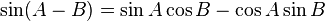
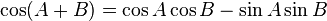

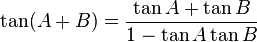
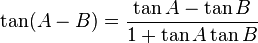



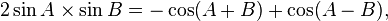













No comments:
Post a Comment